Understanding Chord Inversions

In this tutorial, I'll show you a smart way to use octave intervals for generating chord inversions.

We'll do this process with the help of the fretboard, so our neck navigation skills will improve as well.

What Are Chord Inversions?

If you already studied a bit of chord construction theory, you already know that a chord is formed by three or more notes stacked one on top of another.

Usually, we put the note with the lowest pitch at the bottom; this is the so-called root of the chord and gives the name the chord itself.

For instance, if we have a C at the bottom, the chord is named C "something" chord.

The remaining notes are at different distances from the root.

These distances are called "intervals"

For example, in a major chord, we have the root, a major third, and a perfect fifth.

A major third is 4 half-steps from the root, while a perfect fifth is 7 half-steps.

Back to our C example.

If we stack a major third and a perfect fifth on our C root, we get a C major chord.

The "something" named above is now "major", because we have root, major third, and the perfect fifth.

Each intervals combination has its unique name, check our complete chord formula table here.

Generating Chord Inversions

Depending on which note of the chord is at the lowest position, we can have different configurations:

• Root Position: when we have the root as the lowest note, we say that the chord is in the root position.
• First Inversion: if we move the root up to the upper octave, we have the third as the lowest note. This is called first inversion.
• Second Inversion: again, we move the third to the upper octave, and now we have the fifth in the lowest position. This is called second inversion.

We can easily visualize this process on the fretboard, with a double benefit: understanding the logic behind those triads shapes, and improving fretboard navigation confidence.

I've learned this trick by Ted Greene, the legendary jazz guitar master.

We start with a triad in root position, and we move one note at a time to the upper or lower octave, trying to keep the shape fingering closed (on adjacent strings) and easy to play. Have a look at the images below:

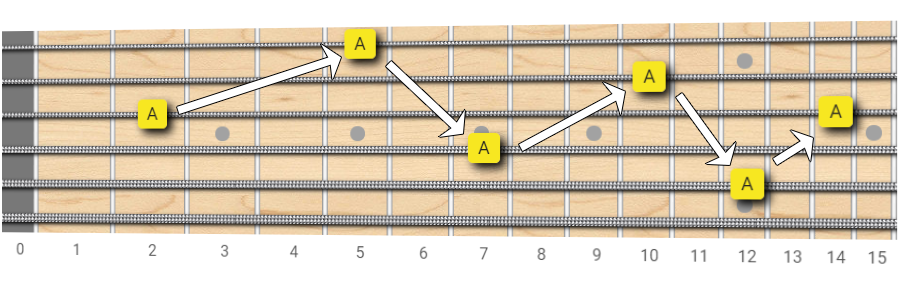
In this first picture, we can see where to find the same note moving horizontally by octave intervals.

Take some time to play these paths and get familiar with them.

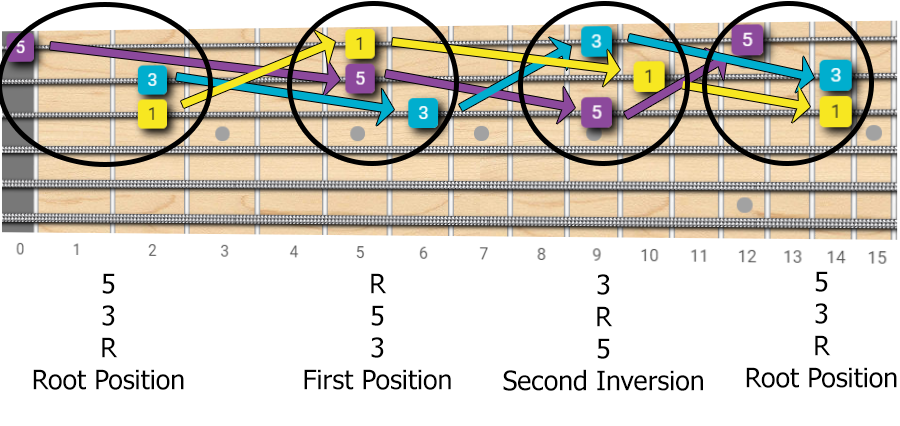
Now we can take a triad shape, and apply this octave trick to all its notes, one at a time.

From the root position, by moving one note at a time, we get the first inversion, then the second, then we go back to the root position.

Again, play these examples on your guitar and listen to the different nuances between the inversions.

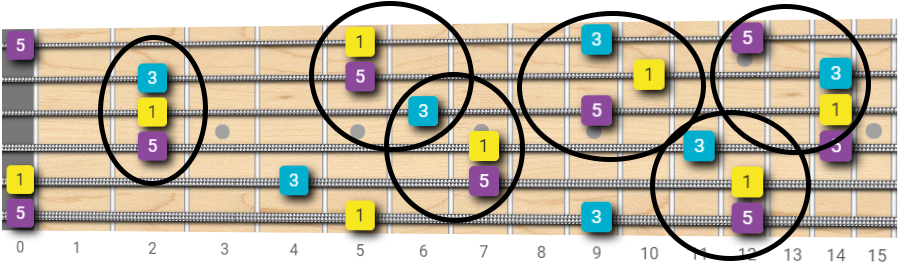
Of course, this method works for each type of triads: major, minor, augmented and diminished, and for all the strings.

Have a look at the diagram below (this time I did not draw the octave arrows to keep the diagrams clearer).

I've highlighted some of the main triad shapes that one can find over the entire fretboard.

See how the root (R), the third (3) and the fifth (5) are interconnected by octave intervals.

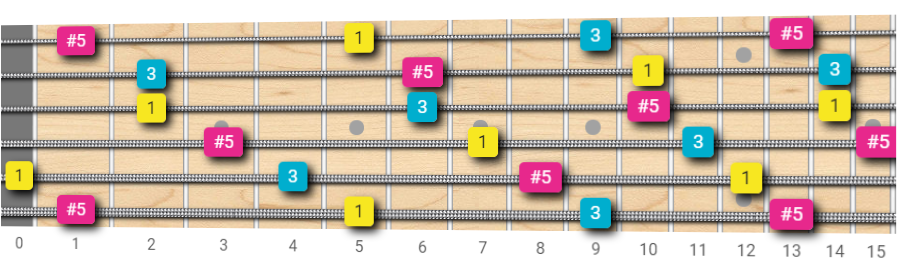
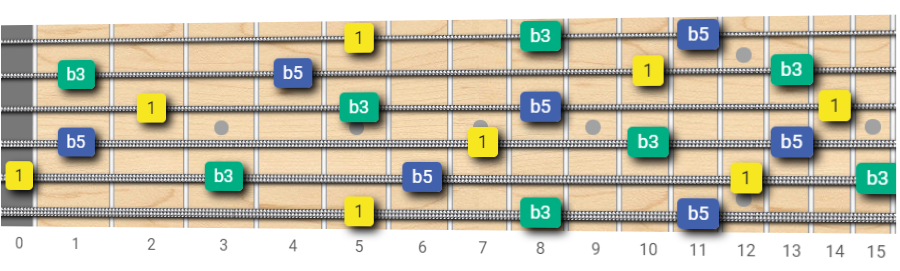
Now it's your turn: use the diagrams below to create your own 3 notes triad-shapes, using octave intervals to move across the fretboard, for the other triad types: minor, diminished, augmented

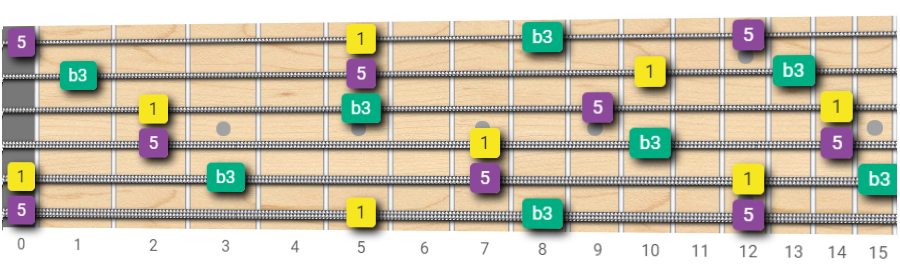
Minor Triads Fretboard Map

A minor triad is composed of the root (R), minor third (b3) and perfect fifth (5).

Augmented Triads Fretboard Map

An augmented triad is composed of the root (R), major third (3) and augmented fifth (#5).

Diminished Triads Fretboard Map

A diminished triad is composed of the root (R), minor third (b3) and diminished fifth (b5).

Four Tones Chords

Now what happens when we deal with four notes chords, such as dominant chord or other types of chord?

The process is the same, but as we have an additional note (usually a 7th interval, major, minor or diminished), and so 4 notes per chord, we can have a third inversion, in which the 7th is at the lowest position.

The diagram below shows you this concept applied to the F major 7th chord.

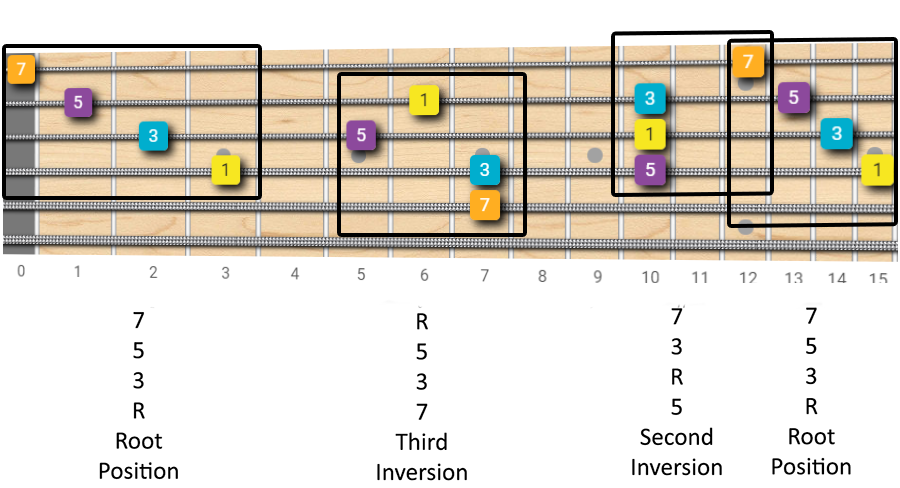
With 4 notes the combinations and thus the complexity explodes, as we have many different options for staking those 4 notes.

But the logic still remains the same.

How Do You Call Fifth Third Root Inversion?

Recently, a FaChords visitor asked a smart question:

Question:

If Fifth Root Third (5 R 3) is a 2nd inversion, what is a Fifth Third Root (5 3 R)??
It's theoretically still a 2nd inversion because of the low 5, but is it??

Answer:

The name of the inversion is decided by the note that is at the bottom, it does not matter the order of the other notes, so 5 R 3 and 5 3 R are called 2nd inversion both.

Chord Inversion: Conclusions and Further References

Unlike the piano keyboard, the guitar fretboard is more complex to understand, as we can play the same note in different places.

Octave intervals are a way to manage this complexity. In my complete ebook "Chords Domination | Play Any Chord You Want Across All The Fretboard ", I go deep in intervals and chord construction, with the help of several full fretboard maps for more than 40 different chord types. Check it out here.

To stay updated on new tutorials, and get access to the free download area, subscribe here.