Moving Chords Up the Fretboard

Hi, in this post we'll see how to move chords up to the neck to create new nuances in our sound. We'll be using our beloved C major chord in open position, which you should already know by heart.

But first, let's see how the C major chord is built:

CEG

The C major chord is composed of the root, the third and the fifth, so we have C, E and G.

Now let's place this chord on the fretboard. I've created an animated diagram that shows you the process step-by-step, please have a look at it and then read the description for each step below.

1) C, the root note of the chord

We have to start from somewhere, so let's begin with the root of the chord, which obviously is C. In this case, the C is taken on the 3rd fret of the A string (if you need help in understanding this, check my guitar fretboard notes tutorial)

2) A chord is made up by 3 notes

As music theory says, a chord is made up of 3 notes. In the case of a major chord, we have the root (C), a major third, which is 4 half-steps from the root, and a perfect fifth, which is 7 half-steps from the root.

Remember that an half-step is exactly a fret, so if you count frets, you'll see that from C to E there are 4 frets, and from C to G there are 7 frets.

3) Octave intervals

On the guitar, unlike the piano, the notes extend horizontally and vertically. We can have the same note on different strings, and this is the most confusing thing for beginners.

In the image, we can see how is possible to find the same note (one-octave higher) by moving 2 frets up the neck and 2 strings up.

4) Octave intervals, part 2

We can also find the same note one string up, and 5 frets below!

That's the reason which the standard method for tuning the guitar requires you to press the a string at the fifth fret, in order to tuner the string right above.

Warning: this does not apply between the 2nd (G) and the 3rd (B) strings, we'll see why later.

5) Now we have a major triad!

By simply placing the 3 notes composing a chord in the same fretboard area, we can play something that reminds our classic C major chord: a major triad!

A major triad is composed of 3 notes: the root, a major third and a perfect fifth (C, E and G in our case)

6) Adding more notes to the triad

We can use the octave interval trick again and place another C on the 2nd string. To find a note one octave higher from the 5th string(A), we can:

• Go up 3 strings and go down 2 frets
• Go up 2 strings, and go up 2 frets (as we've seen before in step 3)

7) Adding the last note

Again, we need to find the octaves of the E on the 4th string (D). We can:

• Go up 2 strings and go up 3 frets
• Go up 3 strings and go down 2 frets (like in step 6)

8) Here we go!

So we have just created our beloved C major chord starting from one note, the root C.

Now let's see how to move this chord up to the fretboard.

9) Moving Up The Fretboard

Now we begin moving up to the fretboard, first thing we do is to find the C and the G on the higher octaves.

10) One More Note Up

We need the fifth, G, to create a major chord. Here's how we find it one octave higher.

11) And Here's A New Shape for The C Major Chord

We have just created the C Major triad, which is a chord made up of 3 notes.

12) Moving Up Further

Again, we place again the root of our chord, C, on higher frets. Using the octave trick, we know that the C is on the 8th fret of the E lower string.

13) Moving the Other Notes

We also move G and E in order to have all the notes in a four frets box

14) Here's Another C Major Chord

Bingo! We have another shape for the C major chord, this time with root on the 8th fret.

15) One More Shape

Now we move G and E on the higher octave, keeping the root (C) on the 8th fret.

16) Moving G on The Lower Octave

We move G on the lower octave, 10th fret of A string.

17) Higher and Lower String have The Same Notes

Finally, we move the C on the fifth fret of G string to the higher octave, which is located on the 8th fret of the higher string. As you maybe already know, the note names on the E high string and E low string are the same!

18) Here's The Full Bar C Major Chord

Hurrah! We just created the C major chord fretted with a full bar fingering. You can shift this 6-strings shape up and down the neck to play a major chord in different roots.

19) The Last Shape

Now we use again octaves to come up with another shape.

20) Here's A C Major Chord Triad in Second Inversion

We have a C Major chord triad with the fifth (G) at the bottom, so we call it the second inversion.

Movable Chord Shapes

Please don't confuse movable chord shapes with creating new fingerings for the same chord up the neck. With movable chord shapes, you shift the whole fingering on different frets, to get the same exact chord with a different root (like a bar chord).

On the contrary, the process of moving chords up the fretboard shown on this page creates new voicings with different inversions and nuances for the same chord and root.

How To Move Chords Up The Fretboard - Conclusions

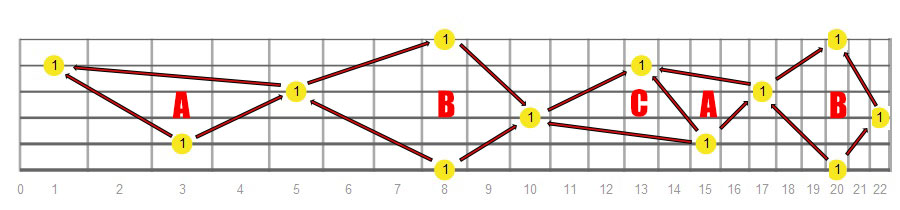
At this point, it should be clear that octave intervals play a crucial role in fretboard exploration. The ability to find a note one octave higher or lower on different fretboard areas will give you great freedom and lots of options.

Here below you find an octave intervals fretboard map, be sure to memorize the shapes (A, B and C) created by the different octaves. Note that these shapes are valid for all the roots, you simply have to place the shapes on the proper note.

You might also find helpful my complete ebook Chords Domination | Play Any Chord You Want Across All The Fretboard, in which I'll show you how to explore the fretboard deeply.

To stay updated, subscribe here