Interval Inversions
Learn How Inversions Work According To The Rule of 9
In this tutorial we're going to learn what are interval inversions.
As a quick refresher, an interval is a distance between two notes, or pitches. Depending on that distance, we'll obtain different sounds and feelings.
Some intervals sound very stable while others are dissonant and unstable. This is the basic palette of a musician.
Basic Intervals Table
If we take the major scale and count each of its note from the root, we get the following intervals:
| Interval | Name | Half-Steps |
|---|---|---|
| C - C | Unison | 0 |
| C - D | Major Second | 2 |
| C - E | Major Third | 4 |
| C - F | Perfect Fourth | 5 |
| C - G | Perfect Fifth | 7 |
| C - A | Major Sixth | 9 |
| C - B | Major Seventh | 11 |
| C - C | Octave | 12 |
Half-steps are also called semitones and correspond to frets on the guitar. 1 half-step = 1 semitones = 1 fret.
Interval Types
By looking at the table below, we notice that computing intervals (so far) is like doing primary school math: we count the notes and get names like Second, Third, Fourth, Fifth, Sixth and Seventh.
The octave interval is a particular one because contains notes with the same names (C and C) but at different pitches (think the same note played with open string and at the 12th fret)
We can also notice the types of intervals: Perfect, Minor, and Major.
So far so good.
But what about intervals of 6 half-steps, 1 half-step, or 8 half-steps? They don't exist on the table.
Well, we have to know that we can also have Diminished and Augmented intervals.
The image below shows you the relationship between all the kinds of intervals:
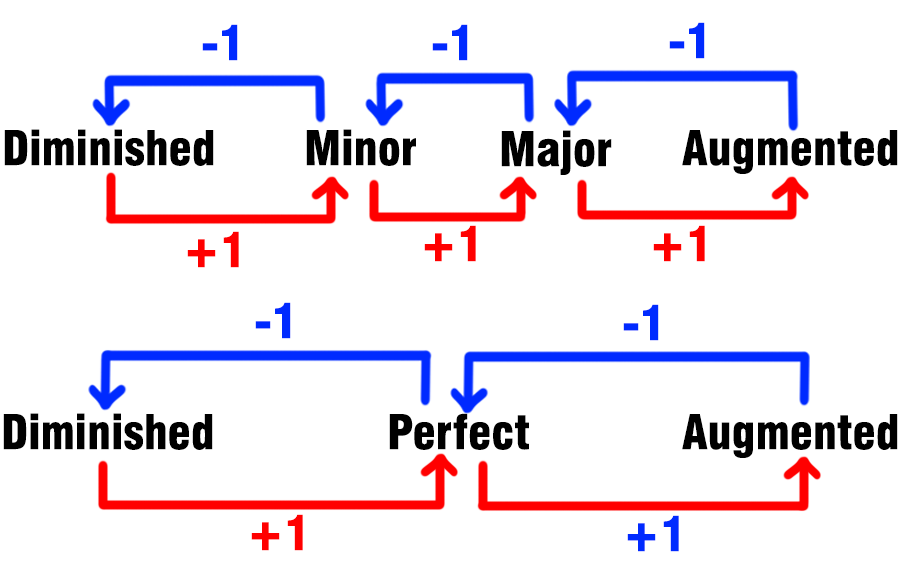
It works in this way:
- The Major Interval lowered by 1 half-step becomes a Minor Interval
- The Minor Interval, raised by 1 half-step, become a Major Interval
- The Perfect Interval, lowered by 1 half-step, becomes a Diminished Interval
- The Perfect Interval, raised by 1 half-step, becomes an Augmented Interval
- The Major Interval, raised by 1 half-step, becomes an Augmented Interval
- The Minor Interval, lowered by 1 half-step, becomes an Diminished Interval
Complete Interval Table
Now we can draw a complete table with all the intervals, with distances from 0 to 12.
| Interval | Example | Half-Steps | Symbol |
|---|---|---|---|
| Unison | (C-C) | 0 | |
| Minor Second | (C-Db) | 1 | |
| Major Second | (C-D) | 2 | |
| Minor Third | (C-Eb) | 3 | |
| Major Third | (C-E) | 4 | |
| Perfect Fourth | (C-F) | 5 | |
| Diminished Fifth / Augmented Fourth | (C-Gb)/(C-F#) | 6 | |
| Perfect Fifth | (C-G) | 7 | |
| Minor Sixth | (C-Ab) | 8 | |
| Major Sixth | (C-A) | 9 | |
| Minor Seventh | (C-Bb) | 10 | |
| Major Seventh | (C-B) | 11 | |
| Octave | (C-C) | 12 |
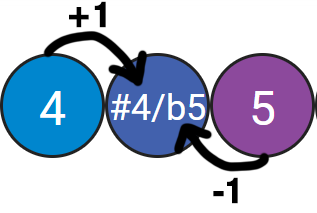
Did you see the row with "Diminished Fifth / Augmented Fourth"? What is this?
We can lower a Perfect Fifth by one half-step and get a Diminished Fifth ( 7 - 1 = 6), or we can raise a Perfect Fourth by one-half step and get an Augmented Fourth (5 + 1 = 6).
Same distance (6), but different names. This music theory strangeness is called enharmonics.
You can also use this fretboard intervals guide to play intervals on the guitar neck.
Interval Inversion
After this quick introduction, we are now ready to learn about interval inversion.
In an interval, an inversion happens when you move the lowest note to the higher octave, or, on the contrary, you move the highest note to the lowest octave.
For example, this is the interval A E (as always on guitar, it's helpful to show this concept on one single string), which is a Perfect Fifth (7 frets):

To get the inverted interval (E A), you can move the A one octave up, or you can move the E one octave below, as the picture below shows:

E A is five half-steps or frets, so it's a Perfect Fourth.
The Rule Of 9
Now it's time to unveil the rule that stays at the foundation of interval inversion: the rule of 9.
The rule of 9 says: the number of any interval and the number of its inversion always add up to nine.
In the example above, we inverted the 5th interval and we got the 4th interval, so 5+4 = 9
Here are other examples:

C-E is a Major Third (4 half-steps), its inversion, E-C, is a Minor Sixth (8 half-steps): 3+6=9

D-E is a Major Second (2 half-steps), E-D is a Minor Seventh (10 half-steps), 2+7=9
We could even think about the rules of 12: the sum of the half-steps in an interval and the half-steps in its inversion always add up to 12 (one octave).
What Happens To Interval Type During Inversion?
You might be wondering how the process of inversion impacts the type of interval. Here's a recap schema:
- When inverted, the Major interval becomes Minor
- The Minor interval becomes Major
- The Perfect interval remains Perfect
- The Diminished interval becomes Augmented
- The Augmented interval becomes Diminished
A Peculiar Interval: The Tritone
The Tritone is an interval 6 half-steps wide. It can have 2 names: Augmented fourth or Diminished Fifth.
The inverted interval of an Augmented Fourth is a Diminished Fifth, and vice-versa. Again, 4+5=9, or 5+4=9.
The particular characteristic of this interval is that it divides exactly the octave in 2 equal parts (12/6=2), and it's the most dissonant interval.
This ends our tutorial on interval inversions. To stay updated and get free access to the free resources, subscribe here.
FAQ
What does it mean to 'invert' an interval on the guitar?
Inverting an interval means shifting one of its notes by an octave. You either move the lower note an octave higher or the upper note an octave lower. On the guitar, this changes the position of the notes on the fretboard while maintaining their musical relationship. For example, a C-E interval (Major Third) can be inverted to an E-C interval (Minor Sixth) by moving the lower C up an octave.
How do the 'Rule of 9' and the 'Rule of 12' help me understand interval inversions?
The 'Rule of 9' dictates how the *numeric name* of an interval changes: the original interval number and its inversion's number will always sum to nine (e.g., a 4th inverts to a 5th, 4+5=9). The 'Rule of 12' refers to the *total half-steps* in an octave. It states that the number of half-steps in an original interval, when added to the number of half-steps in its inversion, will always sum to 12. Both rules describe different aspects of the same inversion process, one for the interval's numerical size and the other for its total distance in semitones.
How do interval qualities (Major, Minor, Perfect, etc.) change when they are inverted?
When an interval is inverted, its quality transforms predictably: Major intervals become Minor, and Minor intervals become Major. Perfect intervals remain Perfect. Diminished intervals transform into Augmented intervals, and conversely, Augmented intervals become Diminished. For example, a Major Third will invert to a Minor Sixth, while a Perfect Fifth will remain a Perfect Fourth (Perfect quality preserved).
Why is the tritone considered a peculiar interval when it comes to inversion?
The tritone is peculiar because it is exactly six half-steps wide, dividing the octave precisely in half. While it can be named as an Augmented Fourth or a Diminished Fifth, its inversion always results in the 'other' tritone (an Augmented Fourth inverts to a Diminished Fifth, and vice versa). Although its specific name changes, the inverted interval still spans six half-steps, making it unique in how its quality and numeric name relate to its inverted form.
How can I practically apply interval inversion on the guitar fretboard?
To apply interval inversion on the guitar, consider an interval like C to G (a Perfect Fifth). If C is on the 3rd fret of the A string and G is on the 3rd fret of the low E string, you can invert it by moving the lower note (C) up an octave. This means playing the G (lower note of the inversion) on the 3rd fret of the low E string and the C (higher note of the inversion) on the 8th fret of the low E string (or 3rd fret of the A string and 5th fret of the G string, depending on string choice). The resulting interval, G to C, is a Perfect Fourth, demonstrating the 'Rule of 9' (5+4=9) and the 'Perfect' quality remaining constant.