Circle Of Fifths Chord Shapes
How To Create All Chord Types With Geometry
This page shows you a peculiar feature of the Circle of Fifths.
The Circle of Fifths is a graphical representation of the relationships of the 12 tones of the chromatic scale.
It shows the relationships between major and minor keys, and can be used to determine the key of a piece of music, identify chord progressions, and modulate from one key to another.
It is also useful for understanding intervals and transposition.
Here we're going to focus of using the Circle of Fifths for chord construction.
Circle Of Fifths and Chord Construction
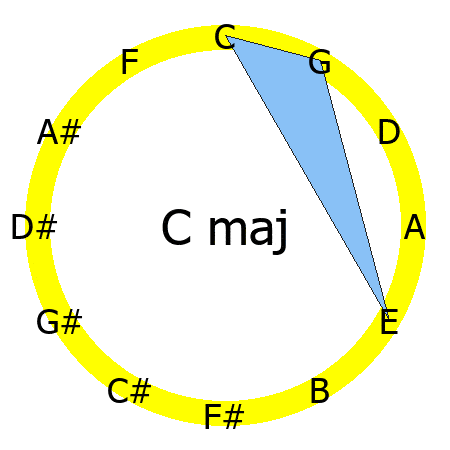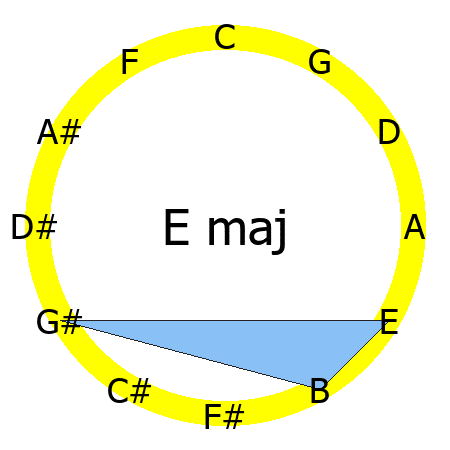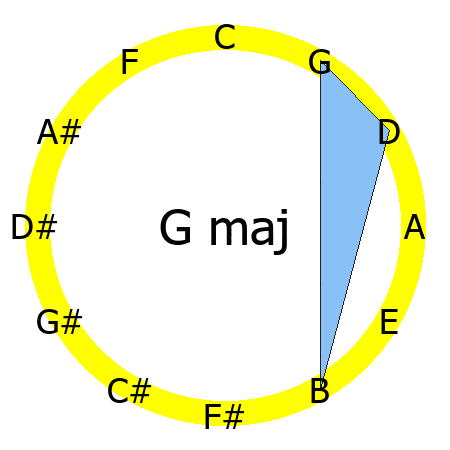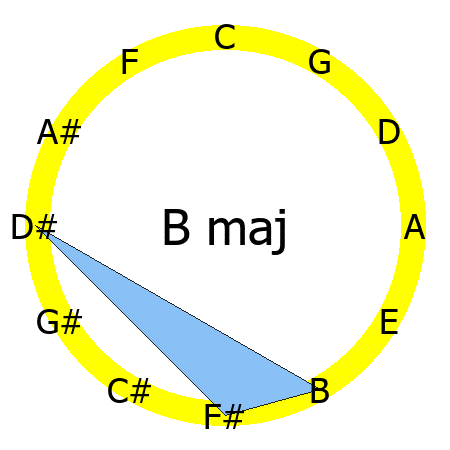 If you create a polygon by connecting the notes that compose a chord, you'll notice that each chord quality has its own specific shape.
If you create a polygon by connecting the notes that compose a chord, you'll notice that each chord quality has its own specific shape.
In this picture, you can see the triangle created by the root, the major third and the fifth.
The curious thing is that the shape of that triangle remains the same for all the major chords.
The animation shows you the triangles created by connecting the notes of C, D, E ,F ,G, A and B major chords.
It's clear now that you only need 2 things for creating a major chord: your Circle of Fifths note sequences, and the shape of the major chord triangle.
Once you have memorized these two things, you can overlay the triangle on the correct root, and know the notes in any major chord.
The great thing is that this trick works for all chord types! In the following, you find the shapes created by all those chords, with C as the root note.
Major chords
Major chords are composed of the root, the major third, and the fifth. In the diagrams below, notice that the power chord (c5, root and perfect fifth), does not create a closed polygon because it has only two points.
Maybe that's the reason why classical music theorist do not consider the power chord as a real chord.
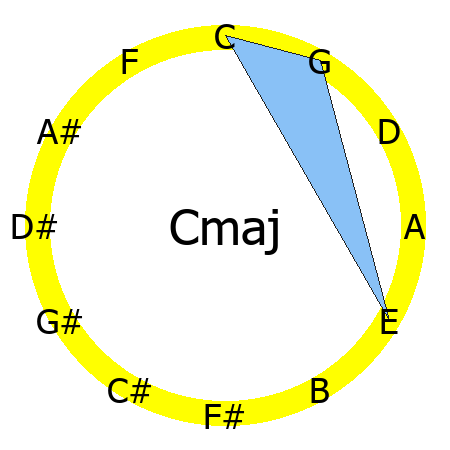
Cmaj chord
Tones: 1, 3, 5
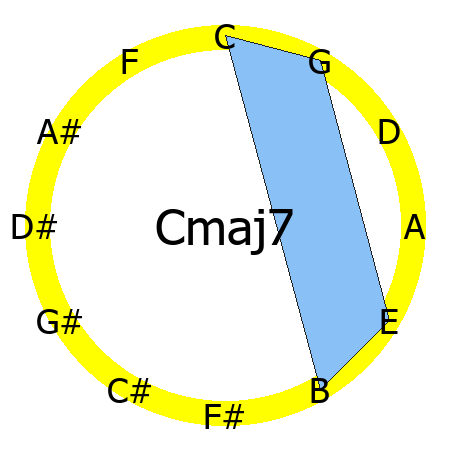
Cmaj7 chord
Tones: 1, 3, 5, 7
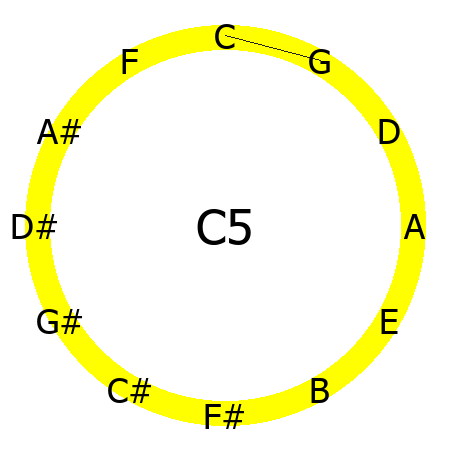
C5 chord
Tones: 1, 5
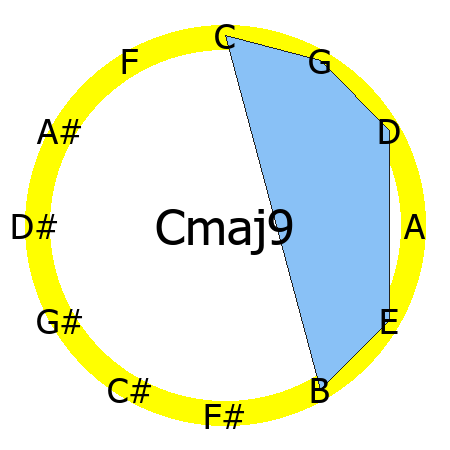
Cmaj9 chord
Tones: 1, 3, 5, 7, 9
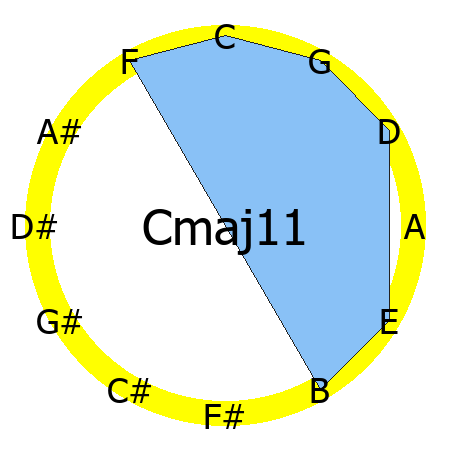
Cmaj11 chord
Tones: 1, 3, 5, 7, 9, 11
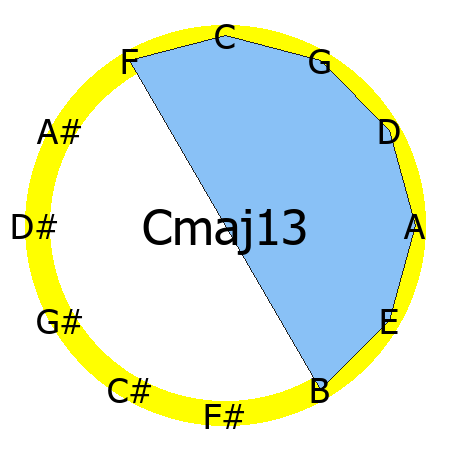
Cmaj13 chord
Tones: 1, 3, 5, 7, 9, 11, 13
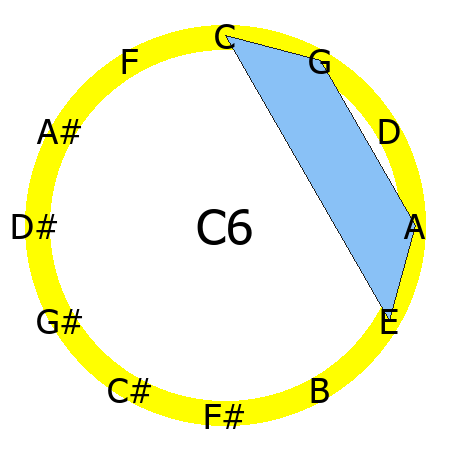
C6 chord
Tones: 1, 3, 5, 6
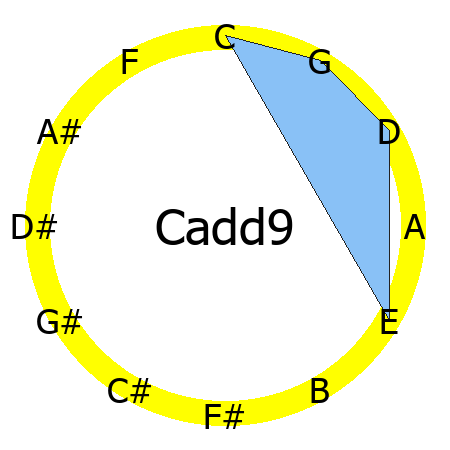
Cadd9 chord
Tones: 1, 3, 5, 9
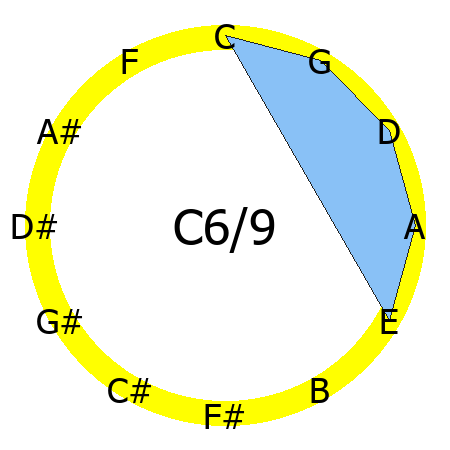
C6/9 chord
Tones: 1, 3, 5, 6, 9
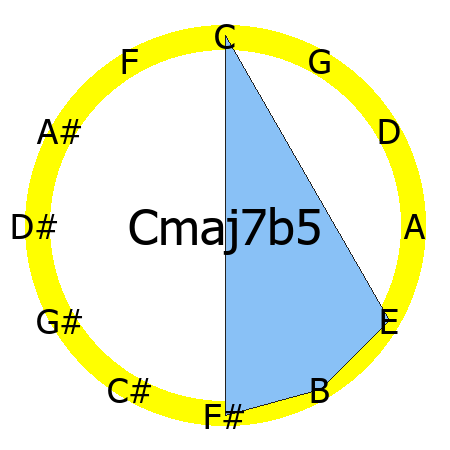
Cmaj7b5 chord
Tones: 1, 3, b5, 7
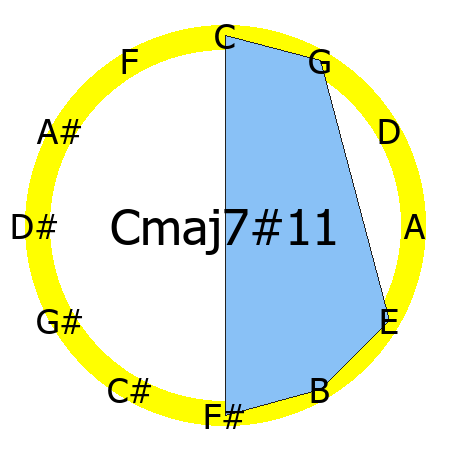
Cmaj7#11 chord
Tones: 1, 3, 5, 7, #11
Suspended chords
Suspended chords do not have the third, which is substituted by a second or a fourth.
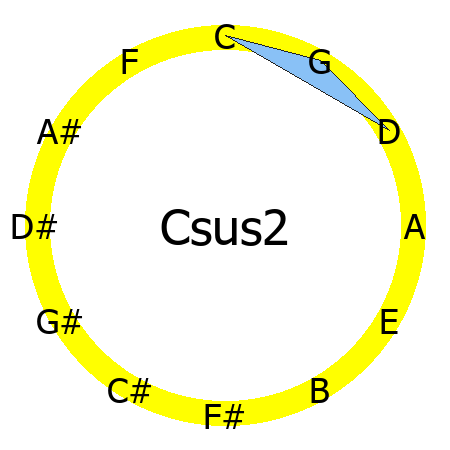
Csus2 chord
Tones: 1, 2, 5
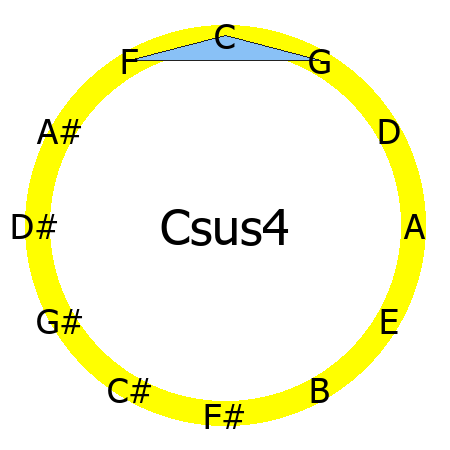
Csus4 chord
Tones: 1, 4, 5
Minor chords
Minor chords are composed of the root, the minor third (contrary to major chords that have the major third), and the fifth.
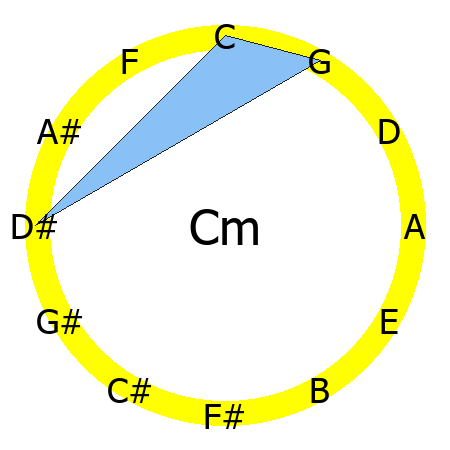
Cm chord
Tones: 1, b3, 5
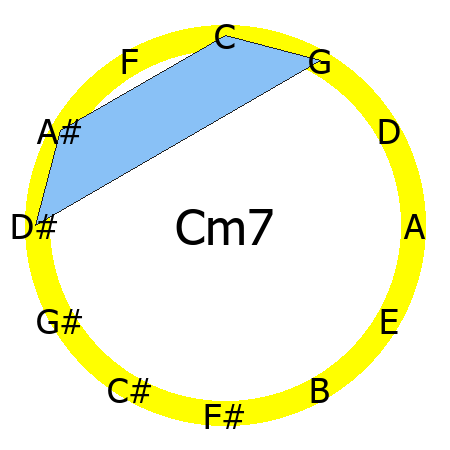
Cm7 chord
Tones: 1, b3, 5, b7
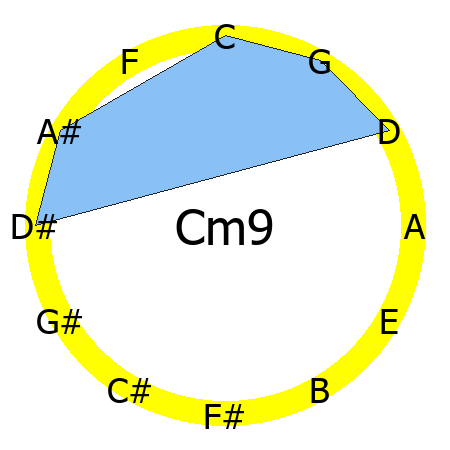
Cm9 chord
Tones: 1, b3, 5, b7, 9
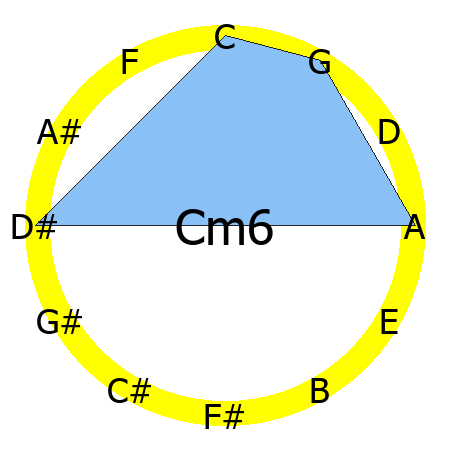
Cm6 chord
Tones: 1, b3, 5, 6
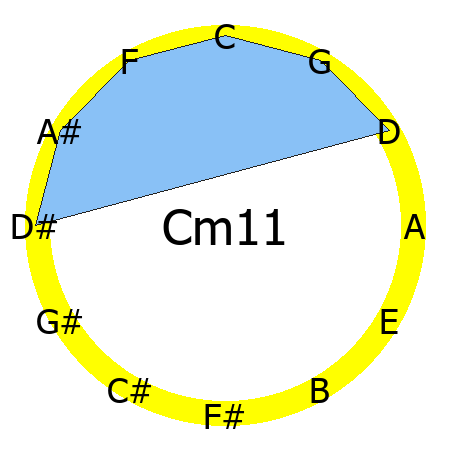
Cm11 chord
Tones: 1, b3, 5, b7, 9, 11
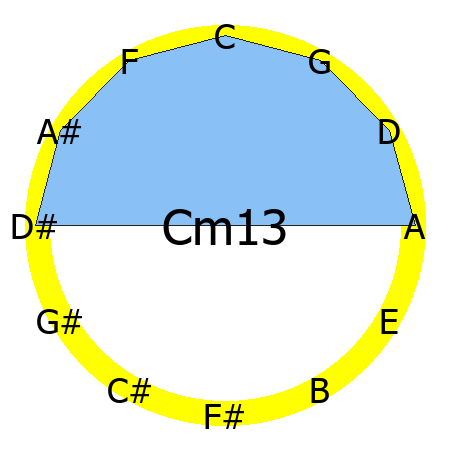
Cm13 chord
Tones: 1, b3, 5, b7, 9, 11, 13
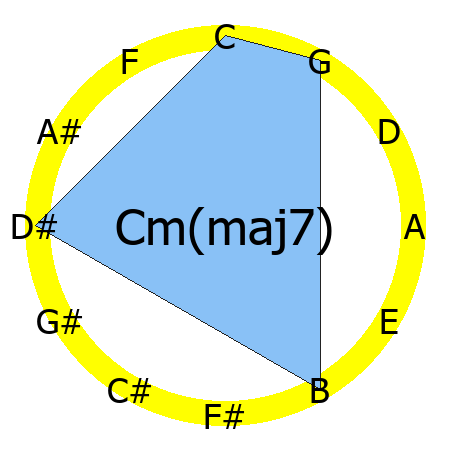
Cm(maj7) chord
Tones: 1, b3, 5, 7
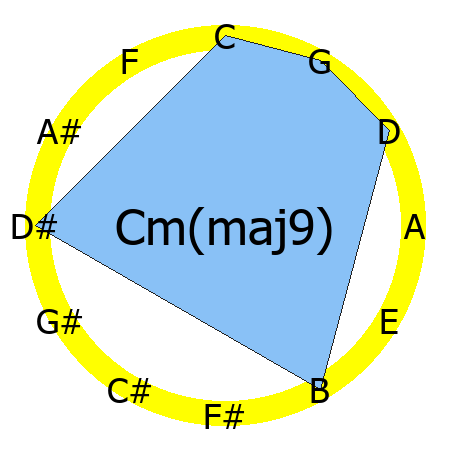
Cm(maj9) chord
Tones: 1, b3, 5, 7, 9
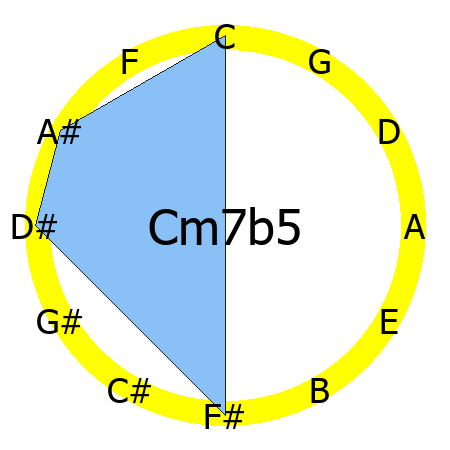
Cm7b5 chord
Tones: 1, b3, b5, b7
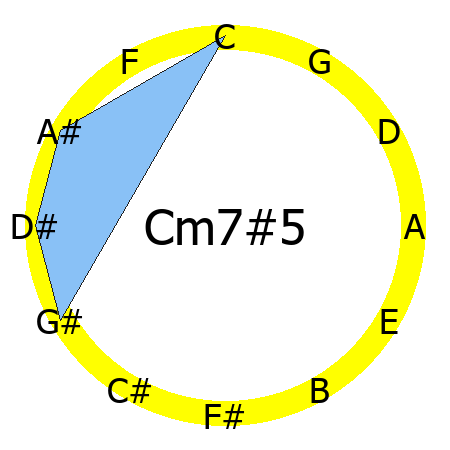
Cm7#5 chord
Tones: 1, b3, #5, b7
Dominant Chords
Dominant chords are major chords with a minor seventh, they have a really unique, dissonant sound, that is used to create tension and resolution in songs.
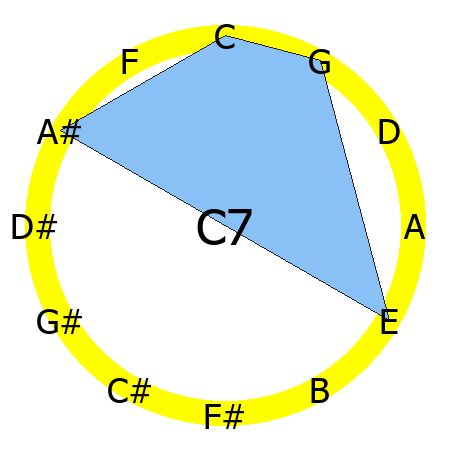
C7 chord
Tones: 1, 3, 5, b7
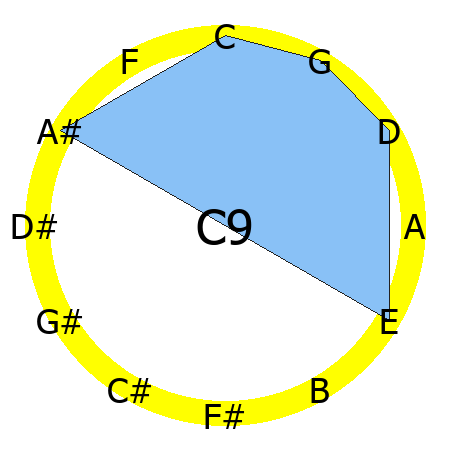
C9 chord
Tones: 1, 3, 5, b7, 9
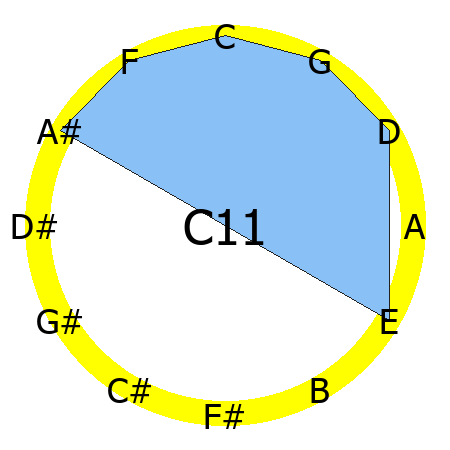
C11 chord
Tones: 1, 3, 5, b7, 9, 11
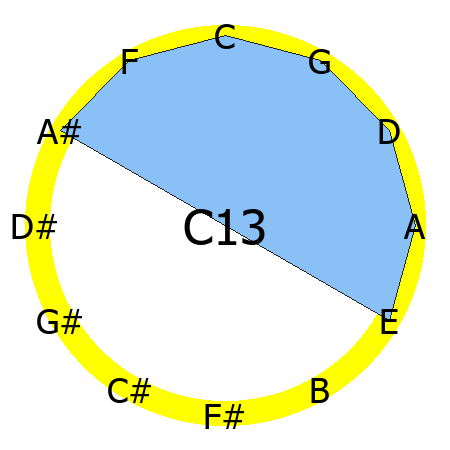
C13 chord
Tones: 1, 3, 5, b7, 9, 11, 13
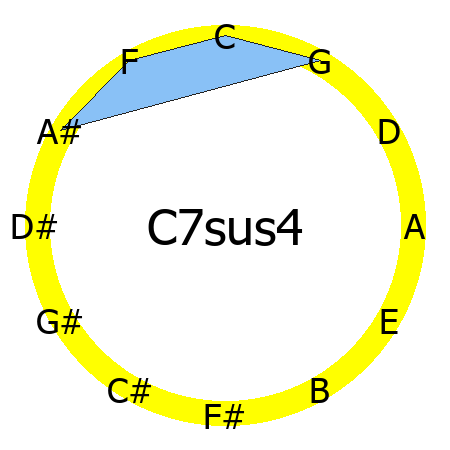
C7sus4 chord
Tones: 1, 4, 5, b7
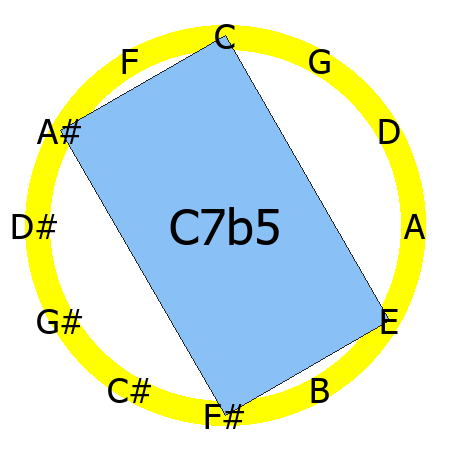
C7b5 chord
Tones: 1, 3, b5, b7
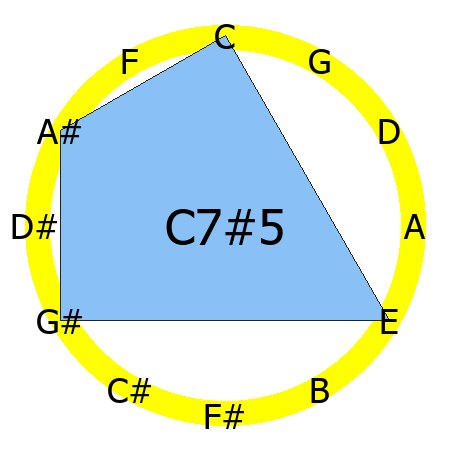
C7#5 chord
Tones: 1, 3, #5, b7
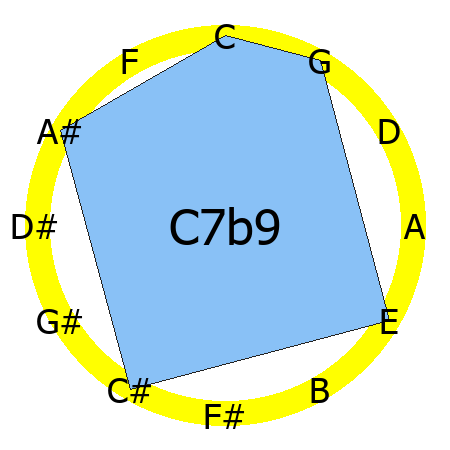
C7b9 chord
Tones: 1, 3, 5, b7, b9
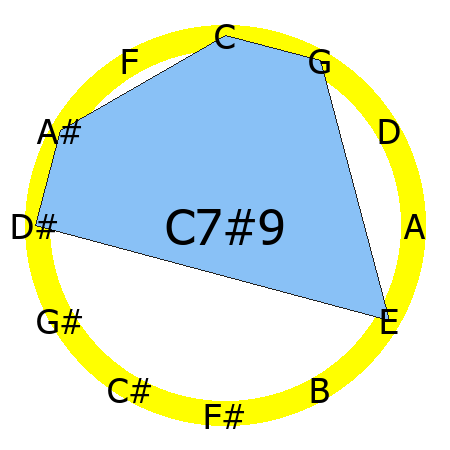
C7#9 chord
Tones: 1, 3, 5, b7, #9
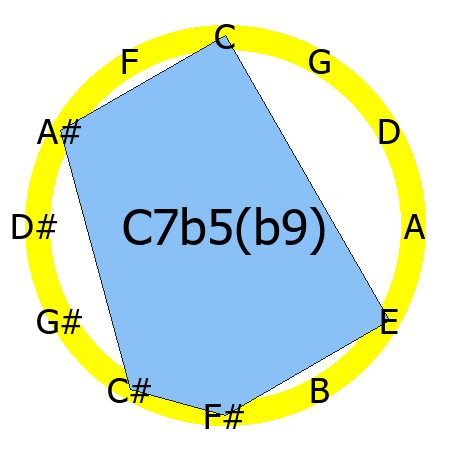
C7b5(b9) chord
Tones: 1, 3, b5, b7, b9
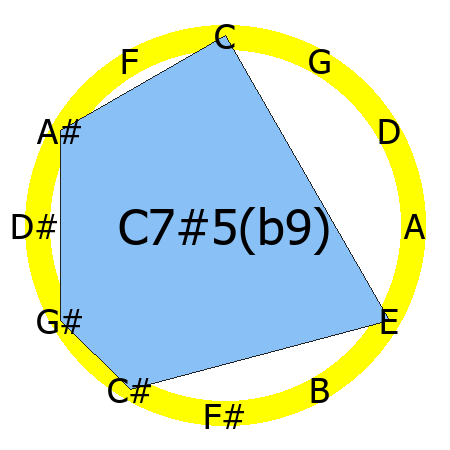
C7#5(b9) chord
Tones: 1, 3, #5, b7, b9
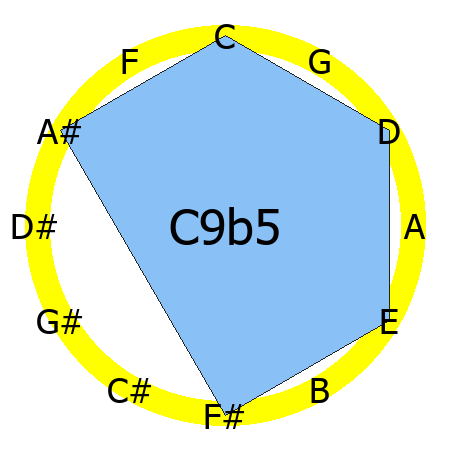
C9b5 chord
Tones: 1, 3, b5, b7, 9
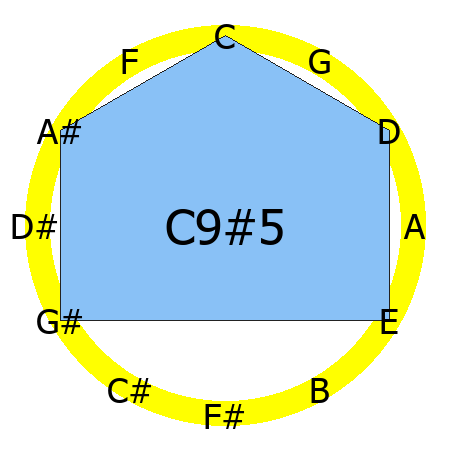
C9#5 chord
Tones: 1, 3, #5, b7, 9
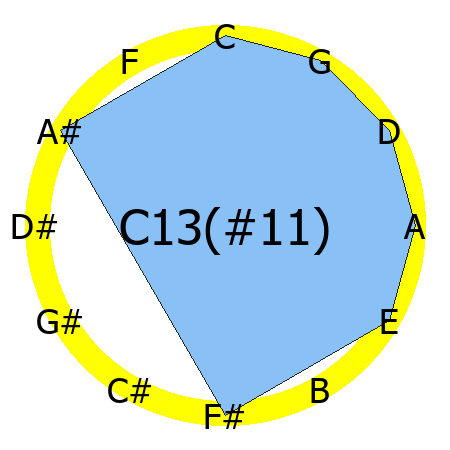
C13(#11) chord
Tones: 1, 3, 5, b7, 9, #11, 13
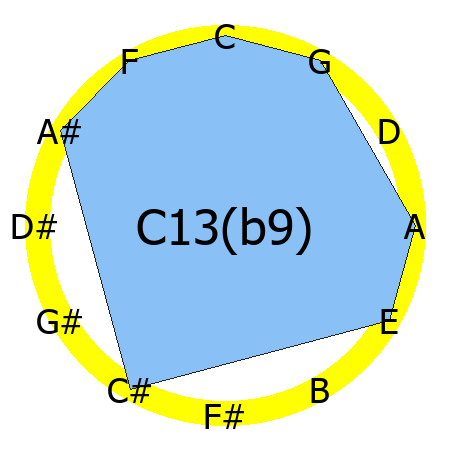
C13(b9) chord
Tones: 1, 3, 5, b7, b9, 11, 13
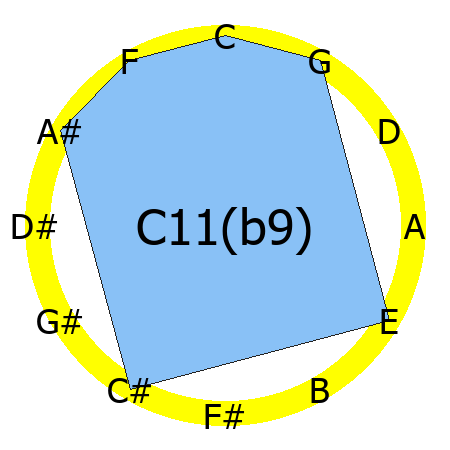
C11(b9) chord
Tones: 1, 3, 5, b7, b9, 11
Augmented and Diminished Chords
Augmented chords are major chords with the fifth raised by one half-step.
Diminished chords are minor chords with the fifth lowered by one half-step.
Notice how augmented (1,3,#5) and diminished (1, b3, b5) chords create beautiful symmetrical shapes.
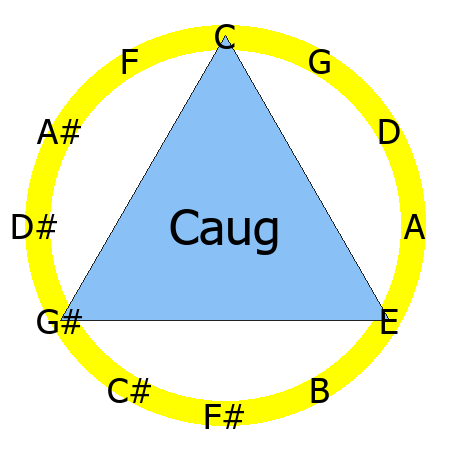
Caug chord
Tones: 1, 3, #5
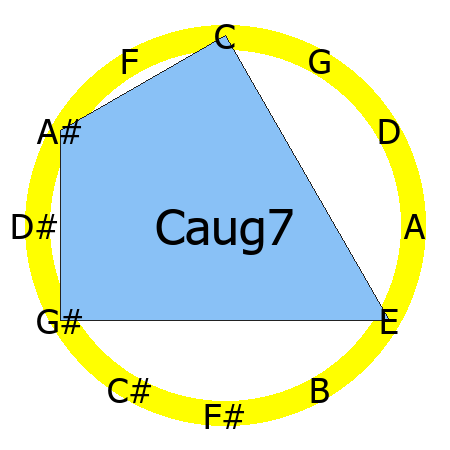
Caug7 chord
Tones: 1, 3, #5, b7
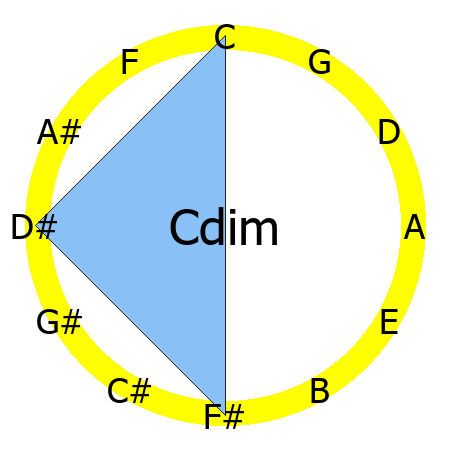
Cdim chord
Tones: 1, b3, b5
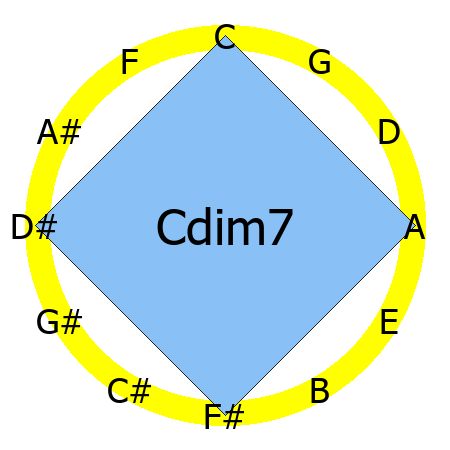
Cdim7 chord
Tones: 1, b3, b5, bb7
Circle Of Fifths Chord Shapes: Conclusion
Ok, in this article, we unveiled some secrets of the Circle of Fifths.
It's a really powerful device, to better understand it, be sure to play around with the Interactive Circle of Fifths hosted on this site.
That's all for today, to stay updated on new learning material, subscribe here.
FAQ
What is the core concept of visualizing chord shapes on the Circle of Fifths?
The core concept is that when you connect the individual notes that make up any given chord on the Circle of Fifths, you will always form a specific geometric shape. What's particularly useful is that this shape remains consistent for a particular chord quality (e.g., all major chords will have the same shape), regardless of the root note.
How does recognizing these Circle of Fifths chord shapes help me as a guitarist?
Once you learn the unique geometric shape for a specific chord type (like a major triad or a dominant seventh), you can identify the notes of that chord in any key. You simply find the desired root on the Circle of Fifths and overlay that memorized shape onto it to reveal the chord's component notes, making chord construction and understanding highly intuitive.
Why don't power chords (C5) create a closed polygon shape on the Circle of Fifths?
Power chords, such as C5, are composed of only two notes: the root and the perfect fifth. Since a closed polygon requires at least three points (vertices), a two-note chord cannot form a closed shape on the Circle of Fifths. This is why some classical music theorists don't consider them 'real' chords in the traditional sense.
What is the difference in appearance between major, minor, and dominant chord shapes on the Circle of Fifths?
While all major, minor, and dominant chords have distinct shapes, their primary differences stem from the quality of their third and seventh intervals. Major chords include a major third, minor chords have a minor third, and dominant chords feature a major third with a minor seventh. These specific interval relationships create unique and consistent geometric patterns for each chord quality when plotted on the Circle of Fifths.
Are there any chord types that form symmetrical shapes on the Circle of Fifths?
Yes, augmented and diminished chords create particularly symmetrical shapes on the Circle of Fifths. An augmented chord (1, 3, #5) forms an equilateral triangle, while a diminished chord (1, b3, b5) also exhibits a distinct symmetry. This visual characteristic helps reinforce their unique intervallic structures.